Performance of Artificial Neural Network Models

for the Prediction of Water Levels

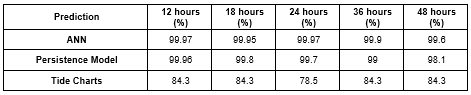
You will find in the tables below a comparison of the ANN performance with the Tide charts and a simple persistence model for 14 stations along the Texas coast. The performance is evaluated using a National Ocean Service standard, the Central Frequency of 15 cm for each model/location, i.e. the percentage of predictions that are within 15 cm of the measured water level. The models are evaluated based on a perfect prog approach for the wind predictions. While the performance of the NAM model was verified to be unbiased and of good quality for the stations below, the predictions are not perfect. Actual ANN water level predictions will be lower depending on the accuracy of the NAM wind predictions.

BIRD ISLAND

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Dr. Philippe Tissot

BOB HALL PIER

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Dr. Philippe Tissot & Sergey Reid

EAGLE POINT

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Samantha Quisenberry

USCG FREEPORT

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Sergey Reid

GALVESTON PLEASURE PIER

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Sergey Reid

INGLESIDE

Model trained on 1 year of hourly data, 2004. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Angelica Villarreal

MANCHESTER HOUSTON

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Cindy Valencia

PACKERY CHANNEL

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Sergey Reid

PORT ARANSAS

Model trained on 1 year of hourly data, 2004. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Angelica Villarreal

PORT ARTHUR

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Sergey Reid

PORT ISABEL

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Angelica Villarreal & Sergey Reid

ROCKPORT

Model trained on 1 year of hourly data, 1998. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Sergey Reid

SABINE PASS

Model trained on 1 year of hourly data, 2004. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Sergey Reid

TEXAS STATE AQUARIUM

Model trained on 1 year of hourly data, 2004. The performance is computed based on 4 years of hourly data (2000-2003).

Central Frequency (% within 15 cm)

Root Mean Square Error (cm)

Optimized by Sergey Reid